728x90
📚문제


📝풀이
def solution(n):
# 배열 생성
array = [[0 for _ in range(n)]for _ in range(n)]
# 시작좌표/방향
# 시계방향으로 돌으므로 처음엔 오른쪽
x, y = 0,0
direc = 'r'
# 3. n * n 만큼 반복(이동)
for i in range(1,n**2+1):
# 4. 시작값 1로 설정
array[x][y] = i
# 5. 진행방향 오른쪽일 때
if direc == 'r':
# 5-1) 인덱스를 벗어나거나 / 5-2) 진행방향에 값이 있을 때
if y + 1 == n or array[x][y+1] !=0:
# 5-3 아래방향으로 전환
direc = 'd'
# 5-4 다음 행으로 넘어가기 위해서 x += 1
x += 1
else:
# 5-5 오른쪽 칸으로 계속 움직이기
y += 1
# 6. 진행방향 아래쪽일 때
elif direc == 'd':
# 6-1) 인덱스를 벗어나거나 / 6-2) 진행방향에 값이 있을 때
if x + 1 == n or array[x+1][y] !=0:
# 6-3 왼쪽방향으로 전환
direc = 'l'
# 6-4 이전 열로 넘어가기 위해서 y -= 1
y -= 1
else:
# 6-5 아래칸으로 계속 움직이기
x += 1
# 7. 진행방향 왼쪽일 때
elif direc == 'l':
# 7-1 진행방향에 값이 있을 때
# (인덱스의[-1]로 가게되면 이미 값이 있는 경우와 똑같기 때문에 따로 적지 않는다)
if array[x][y-1] !=0:
# 7-2 위쪽방향으로 전환
direc = 'u'
# 7-3 이전 행으로 넘어가기 위해서 x -= 1
x -= 1
else:
# 7-4 왼쪽칸으로 계속 움직이기
y -= 1
# 8. 진행방향 위쪽일 때
elif direc == 'u':
# 8-1 진행방향에 값이 있을 때
# (인덱스의[-1]로 가게되면 이미 값이 있는 경우와 똑같기 때문에 따로 적지 않는다)
if array[x-1][y] !=0:
# 8-2 오른쪽방향으로 전환
direc = 'r'
# 8-3 다음 열로 넘어가기 위해서 y += 1
y += 1
else:
# 8-4 위칸으로 계속 움직이기
x -= 1
return array전에 코딩테스트 봤을 때도 이런 유형의 문제가 나왔었는데 너무 어려워서 손도 못댔었다
이런 류의 문제를 풀 때 보통 2가지를 이용한다고 한다
1) dx,dy 테크닉

2) 모듈러 연산
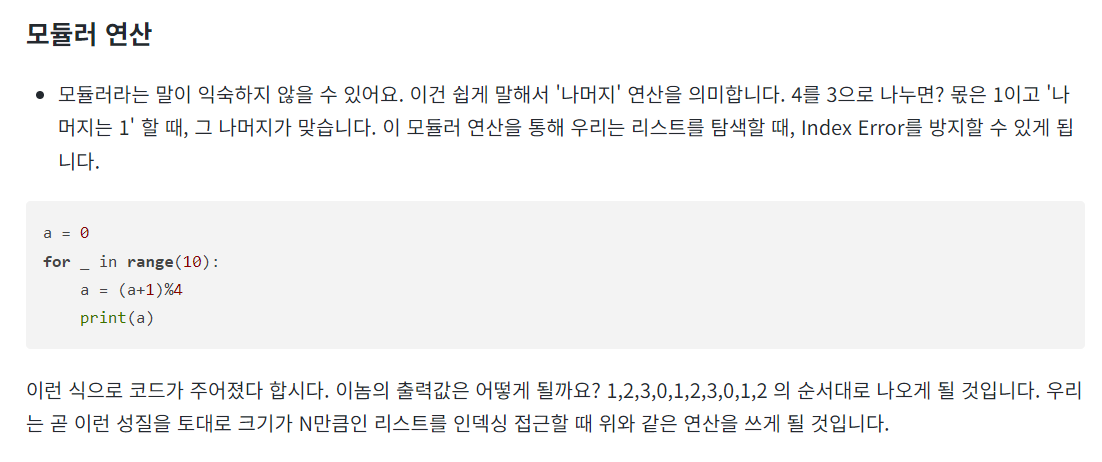
대략 이런 개념들인데
dx,dy 테크닉은 DFS/BFS(깊이우선탐색/너비우선탐색) 개념과도 관련이 있는 것 같다
개념 관련하여 잘 정리해놓으신 글이 있어서
링크를 남겨놓고 나중에 천천히 봐야겠다
▼dx,dy 테크닉
이번 문제는
구글링해서 찾은 풀이들 중에 제일 정확히 이해가 되고 상대적으로 쉬운 풀이를 참고하였고
코드마다 간략한 설명을 첨부해놨다
728x90
'Python(알고리즘,문제풀이) > 프로그래머스(코딩기초트레이닝)' 카테고리의 다른 글
| ***코딩기초트레이닝 / 문자열 묶기 - 파이썬*** (0) | 2023.11.01 |
|---|---|
| 코딩기초트레이닝 / 빈 배열에 추가,삭제하기 - 파이썬 (POP) (0) | 2023.10.31 |
| 코딩기초트레이닝 / 특정 문자열로 끝나는 가장 긴 부분 문자열 찾기(rindex) (0) | 2023.10.27 |
| 코딩기초트레이닝 / 조건에 맞게 수열 변환하기2 - 파이썬 (0) | 2023.10.25 |
| 코딩기초트레이닝 / 가까운 1찾기 (0) | 2023.10.18 |



